Ekspresi adalah kombinasi dari *operand* (nilai atau variabel) dan *operator*
yang menghasilkan nilai baru.
Contoh Ekspresi:
5
+
3
=
8
Di sini, '5' dan '3' adalah *operand*, dan '+' adalah
*operator*. Coba bayangkan ini seperti operasi matematika dasar!
Jenis-jenis Operator:
Jenis Operator
Contoh
Deskripsi
Aritmetika
`5 + 3`, `10 / 2`
Penjumlahan, pengurangan, perkalian, pembagian.
Relasional
`x > y`, `a == b`
Membandingkan dua nilai (menghasilkan *true* atau *false*).
Logika
`A AND B`, `NOT C`
Menggabungkan ekspresi boolean (AND, OR, NOT).
1. Ekspresi dan Operator (Lanjutan)
Tabel Kebenaran Operator Logika
A
B
NOT A
A AND B
A OR B
True
True
False
True
True
True
False
False
False
True
False
True
True
False
True
False
False
True
False
False
Coba Evaluasi Ekspresi Anda Sendiri! (Operator Aritmetika &
Relasional)
Hasil
Masukkan dua angka dan pilih operator untuk melihat
hasilnya!
Coba Evaluasi Ekspresi Logika Anda Sendiri!
Hasil
Pilih nilai True/False untuk A dan B, lalu pilih operator
logika. Jika memilih 'NOT', nilai B akan diabaikan dan hanya A yang dievaluasi.
2. Algoritma
Klik pada elemen-elemen di bawah untuk melihat penjelasan lebih lanjut atau berinteraksi!
Berikut adalah contoh *flowchart* sederhana untuk menghitung luas lingkaran.
Masukkan nilai jari-jari (r) dan klik "Mulai Simulasi" untuk melihat prosesnya!
Mulai
Masukkan nilai r
Hitung nilai Luas L = p * r kuadrat
Tampilkan Luas L
Selesai
Klik pada setiap kotak *flowchart* untuk melihat
penjelasannya!
2. Algoritma (Catatan Penting)
Apa Itu Algoritma?
Algoritma adalah suatu prosedur sistematis untuk menyelesaikan masalah
matematika dalam langkah-langkah terbatas atau urutan pengambilan keputusan yang logis untuk memecahkan
masalah tersebut.
Mengapa Algoritma Penting? (Manfaat Algoritma):
💡 Membantu memecahkan masalah dengan cara yang logis dan sistematis.
♻️ Algoritma dapat digunakan lebih dari satu kali untuk menyelesaikan
masalah yang sama.
🧩 Algoritma juga dapat digunakan untuk membantu memecahkan masalah yang
kompleks dengan lebih sederhana.
🐞 Bagi programmer, algoritma akan memudahkan mereka untuk melacak setiap
kesalahan yang muncul.
✍️ Memungkinkan pemrograman untuk dengan mudah memodifikasi program tanpa
mengubah total algoritma dan tanpa harus mengulang dari awal.
Jenis-Jenis Algoritma yang Perlu Anda Tahu:
➡️Algoritma Sekuensial:
Langkah-langkah dieksekusi secara berurutan, satu demi satu, dari awal hingga akhir. Ini adalah
jenis algoritma yang paling sederhana!
❓Algoritma Kondisional
(Seleksi): Ada keputusan yang harus diambil! Algoritma ini akan memilih jalur eksekusi
berdasarkan kondisi tertentu (misalnya, jika A benar, lakukan X; jika tidak, lakukan Y).
Contoh Interaktif: Cek Angka Positif/Negatif
🔄Algoritma Perulangan
(Looping): Sebuah blok instruksi diulang berkali-kali sampai kondisi tertentu terpenuhi.
Sangat efisien untuk tugas yang berulang!
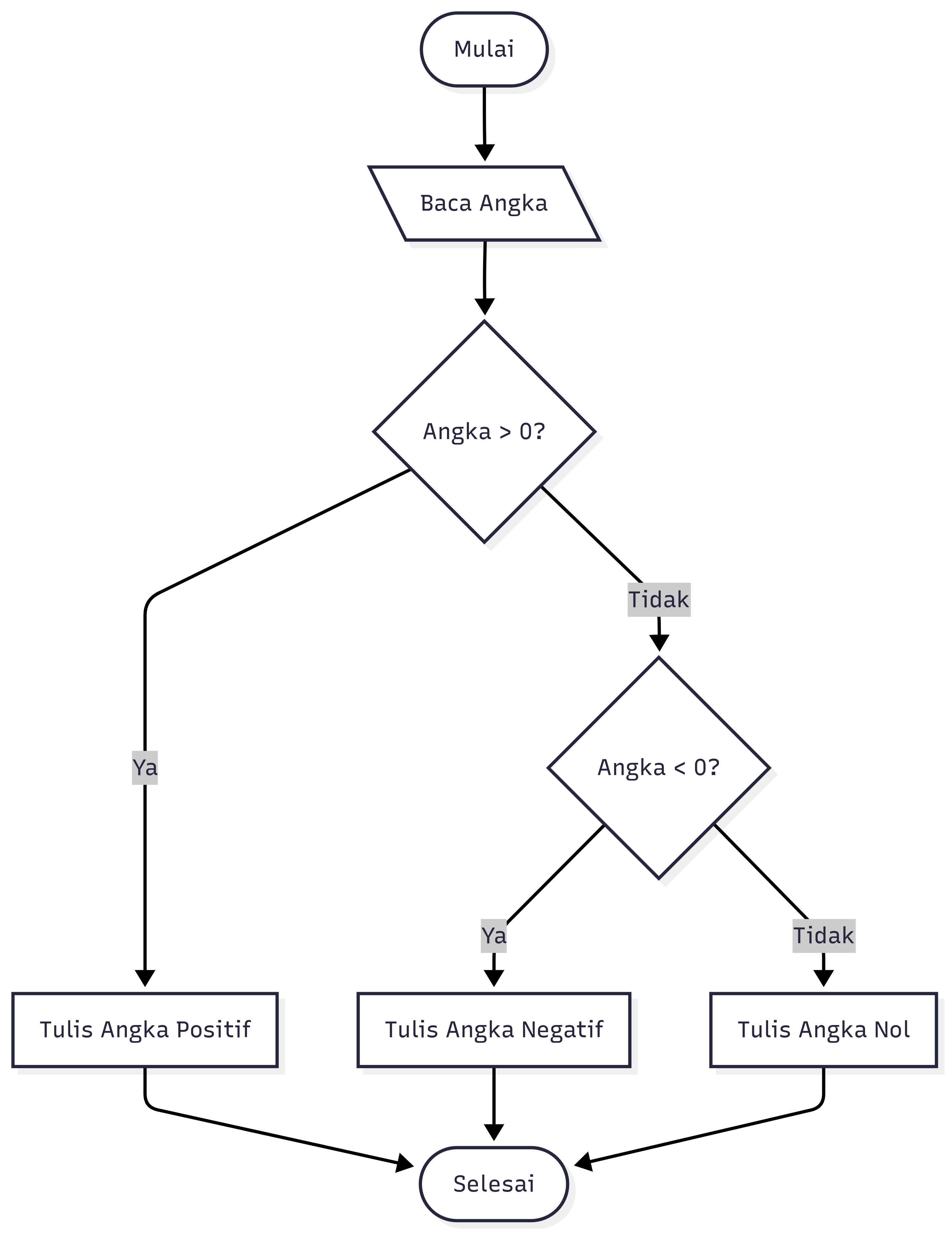
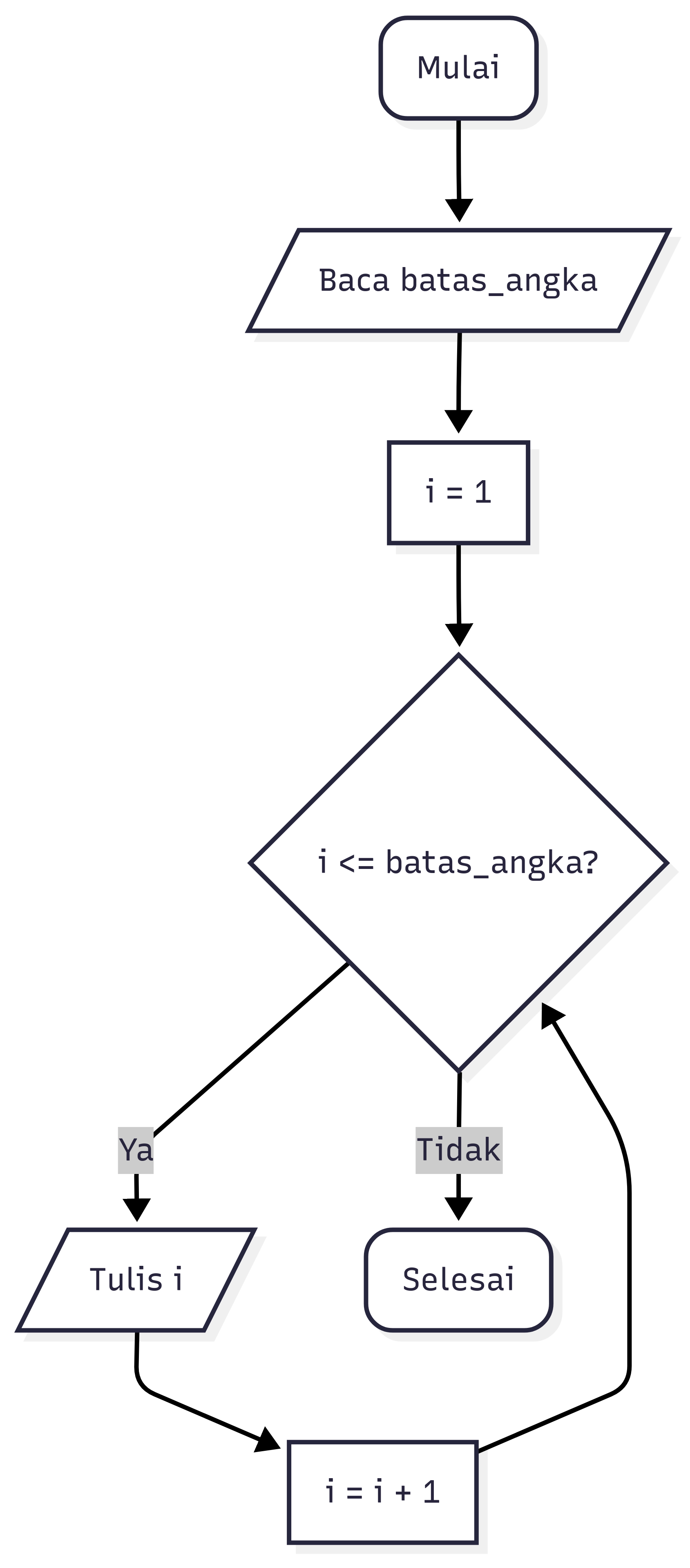
Contoh Interaktif: Hitung Sampai Angka
Bagaimana Kita Menyajikan Algoritma? Ada 3 Cara Utama yang
Menarik!
📝Deskriptif: Menggunakan
bahasa sehari-hari untuk menjelaskan langkah-langkahnya. Mudah dipahami, tapi kurang detail untuk
pemrograman.
💻Pseudocode: Menggunakan
campuran bahasa manusia dan sintaks pemrograman sederhana. Ini seperti "kode palsu" yang mudah
dibaca manusia dan dapat dengan mudah diterjemahkan ke bahasa pemrograman.
Contoh Pseudocode (Cek Angka):
START
BACA angka
JIKA angka > 0 MAKA
TULIS "Angka Positif"
JIKA TIDAK JIKA angka < 0 MAKA
TULIS "Angka Negatif"
JIKA TIDAK
TULIS "Angka Nol"
SELESAI
Contoh Pseudocode (Perulangan):
START
BACA batas_angka
UNTUK setiap i DARI 1 HINGGA batas_angka LAKUKAN
TULIS i
SELESAI
SELESAI
📊Flowchart (Diagram Alir):
Menggunakan simbol grafis standar untuk merepresentasikan langkah-langkah dan alur logika. Visual
dan sangat intuitif! Anda bisa melihat contoh *flowchart* interaktif di .
3. Struktur Data
a. Stack (Tumpukan) - LIFO (Last In, First Out)
Bayangkan ini seperti tumpukan piring. Piring yang terakhir Anda
letakkan adalah yang pertama Anda ambil!
b. Queue (Antrian) - FIFO (First In, First Out)
Ini seperti antrian di bank. Orang yang pertama datang adalah yang
pertama dilayani!
3. Struktur Data (Lanjutan)
c. Graph
Graph terdiri dari simpul (*vertex*) dan sisi (*edge*) yang menghubungkannya.
Klik pada simpul untuk melihat detailnya!
A
B
C
D
3. Struktur Data (Lanjutan)
d. Tree
Struktur data hierarki dengan simpul akar, simpul anak, dan daun. Klik pada
simpul untuk melihat detailnya!
A (Root)
B
C
D
E
F
G (Leaf)
H (Leaf)
3. Struktur Data (Kegunaan)
Kegunaan Graph dan Tree dalam Kehidupan Sehari-hari
Struktur data Graph dan Tree mungkin terdengar abstrak, tetapi keduanya
memiliki peran yang sangat penting dalam berbagai aplikasi di sekitar kita:
🔗Graph:
👥Media Sosial: Jaringan
pertemanan Anda di Facebook atau koneksi di LinkedIn adalah contoh Graph. Setiap orang
adalah simpul, dan hubungan pertemanan/koneksi adalah sisi.
🗺️Peta dan Navigasi: Google
Maps menggunakan Graph untuk menemukan rute terpendek. Kota-kota adalah simpul, dan jalanan
adalah sisi.
🌐Jaringan Komputer: Bagaimana
internet bekerja? Itu adalah Graph raksasa di mana komputer adalah simpul dan koneksi adalah
sisi.
🛒Rekomendasi Produk: Situs
belanja online menggunakan Graph untuk merekomendasikan produk yang mungkin Anda suka
berdasarkan apa yang dibeli orang lain.
🌳Tree:
📁Sistem File Komputer:
Struktur folder dan file di komputer Anda adalah contoh Tree. Folder utama adalah akar, dan
sub-folder serta file adalah cabangnya.
🏢Struktur Organisasi
Perusahaan: Hierarki jabatan dari CEO hingga karyawan paling bawah sering
digambarkan sebagai Tree.
📄Situs Web (DOM): Struktur
halaman web yang Anda lihat (Document Object Model) adalah Tree, di mana elemen HTML
bersarang satu sama lain.
🧠Pohon Keputusan (Decision
Trees): Digunakan dalam Kecerdasan Buatan untuk membuat keputusan berdasarkan
serangkaian kondisi, seperti dalam diagnosis medis atau klasifikasi data.
Jadi, Graph dan Tree adalah fondasi di balik banyak
teknologi yang kita gunakan setiap hari!
